分析

这道题一看就是道小学奥数数论题（因为是数论，所以后文中的除法默认向下取整），直接根据题面硬想是很难想出结论的。尝试通过数据范围分析，第一档部分分直接暴力枚举所有的时间点即可，第二档部分分更为简单，稍加分析就知道答案应该是 $\dfrac{q+1}{2}$，第三档部分分 $p$,$q$ 互质，我们暂时还不知道这有什么用。数据范围很大提示了做法有可能是很结论的东西，本题的输入又只有两个数，那么我们不妨先写暴力打表找规律（大不了最后拿 $5$ 个点离场，这也是比赛的策略）：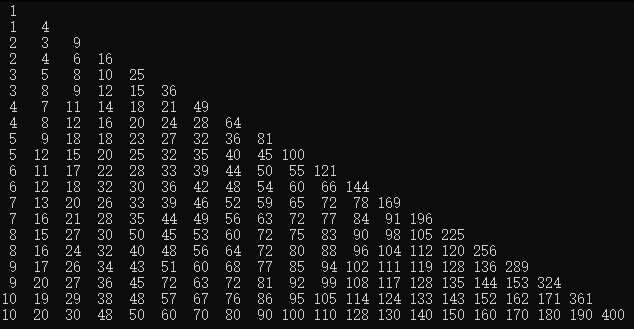

这是 $20$ 及以内的答案，可以看到第一列就是第二档部分分，和前面分析出来的一样。第二行感觉挺有规律但又不是完全有规律，除了一些位置的值比较奇怪，其他位置的值就是 $q$ 的值，那些比较奇怪的位置的 $q$ 的值都是偶数。对 $gcd$ 比较敏感的人就会发现，这些位置上 $gcd(p,q)=2$，而其他位置 $gcd(p,q)=1$，也就是第三档部分分中说的互质。这下我们更加明确在互质的条件下，答案会有一定的性质了，再继续分析剩下的几列（既可以竖着分析，也可以横着分析），不难发现，互质的位置答案就是 $\dfrac{pq+1}{2}$，那么不互质的位置怎么办呢？比如当 $p=4,q=6$ 时，以 $1$ 表示绿灯亮，$0$ 表示红灯亮：

111100001111000011110000……

111111000000111111000000……

用小学奥数知识可以得知后面都是循环的，周期长度$T=lcm(4*2,6*2)=24$，这边只放出了第一个周期。我们再观察一下当 $p=2,q=3$ 时的例子：

110011001100

111000111000

已经写完了，但如果继续往下写，那必然也是循环的，对比一下上一个例子，很显然，这个例子的答案刚好是上个例子一个周期答案的一半，因为它相当于是把每一堆 $1$ 和每一堆 $0$ 的数量都除以 $gcd(4,6)=2$，而上个例子有 $\dfrac{2*4*6}{T}=\dfrac{2*4*6}{4*2*6*2/gcd(4*2,6*2)}=2$ 个周期，所以上一个例子的答案就应该是这个例子的答案的 $4$ 倍。我们得到了 $ans(p,q)=ans(\dfrac{p}{gcd(p,q)},\dfrac{q}{gcd(p,q)})$，然后我们就可以把不互质的位置转化成互质的位置了

代码

这样就可以得出最后的代码了，时间复杂度 $O(log_2(max(p,q)))$，瓶颈在计算 $gcd$ 上。

#include<bits/stdc++.h>
using namespace std;
long long f(long long a,long long b)//互质时的答案
{
    return (a*b+1)/2;
}
long long gcd(long long a,long long b)//最大公约数
{
    return b?gcd(b,a%b):a;
}
int main()
{
    long long a,b;
    cin>>a>>b;
    cout<<f(a/gcd(a,b),b/gcd(a,b))*gcd(a,b)*gcd(a,b);//转化成互质的情况求解
    return 0;
}

证明（思路由 神·@zhaohaikun 提供）

如果你在比赛，在得出这么一份优雅的代码，还通过了对拍之后，这题就算结束了，但练习时，我们还必须知道其中的原理（如果实力允许的话）

如何证明互质的位置答案就是 $\dfrac{pq+1}{2}$？我们先把问题转化为数论的语言。一个时间点 $t$，如果这个时间点两个红绿灯都是绿的，那么 $t$ 应该满足：

$$\left \{ \begin{array}{c} t \leq p \pmod {2p} \\ t \leq q \pmod {2q} \end{array} \right. $$

这是一个线性同余不等式组，如果模数 $p$ 和 $q$ 不互质，我们就得使用 扩展中国剩余定理（EXCRT） 解决。幸运的是，我们已经把模数变为了互质的了，我们只需要使用 中国剩余定理（CRT） 就可以解决。

（待填）